Cross Product Two Dimensions Parkertinsalinas

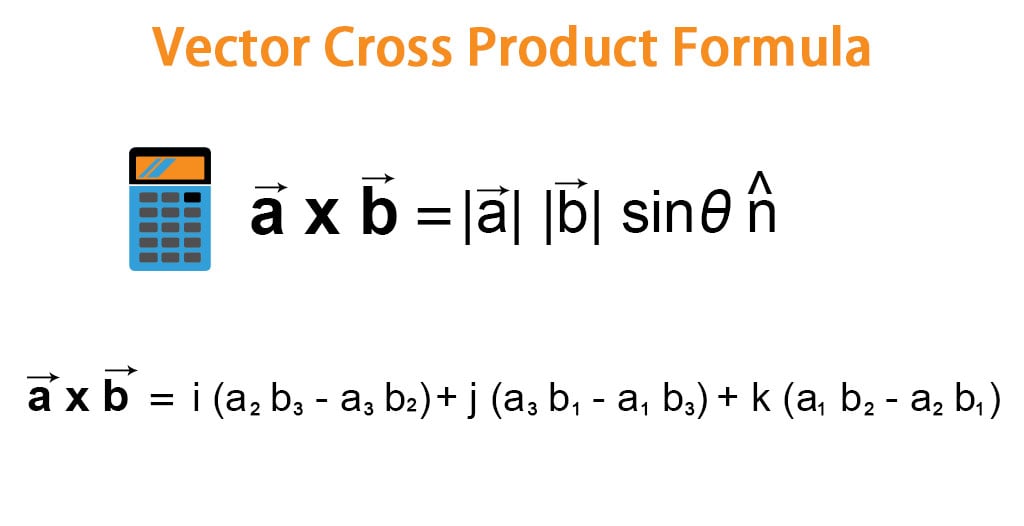
Cross Product Two Dimensions Parkertinsalinas Cross product of two vectors explained click on the get calculation button to get the value of cross product the cross product of two vectors say a b is equal to another vector at right angles to both and it happens in the three dimensions. and it all happens in 3 dimensions. the right hand rule is also. 6. the cross product in 2 dimensions is a scalar give my a 2x2 determinant: (a, b) × (c, d) =∣∣∣a c b d∣∣∣ = ad − cb. the cross product in 3 dimensions is a vector given by the 3x3 determinant: (a, b, c) × (d, e, f) =∣∣∣∣∣ex a d ey b e ez c f ∣∣∣∣∣. e. a. abbott describes a 2d cross product nicely in his.

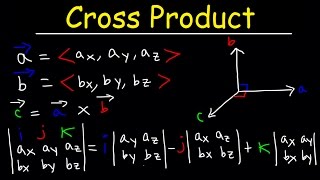
Cross Product Two Dimensions Parkertinsalinas In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three dimensional oriented euclidean vector space (named here ), and is denoted by the symbol . given two linearly independent vectors a and b, the cross product, a × b. The cross product (purple) is always perpendicular to both vectors, and has magnitude zero when the vectors are parallel and maximum magnitude ‖ ⇀ a‖‖ ⇀ b‖ when they are perpendicular. (public domain; lucasvb). example 12.4.1: finding a cross product. let ⇀ p = − 1, 2, 5 and ⇀ q = 4, 0, − 3 (figure 12.4.1). You may already be familiar with the dot product, also called the scalar product. this product leads to a scalar quantity that is given by the product of the magnitudes of both vectors multiplied by the cosine of the angle between the two vectors. as for the cross product, it is a multiplication of vectors that leads to a vector. First, the cross product isn’t associative: order matters. next, remember what the cross product is doing: finding orthogonal vectors. if any two components are parallel ($\vec{a}$ parallel to $\vec{b}$) then there are no dimensions pushing on each other, and the cross product is zero (which carries through to $0 \times \vec{c}$).

Cross Product Two Dimensions Parkertinsalinas You may already be familiar with the dot product, also called the scalar product. this product leads to a scalar quantity that is given by the product of the magnitudes of both vectors multiplied by the cosine of the angle between the two vectors. as for the cross product, it is a multiplication of vectors that leads to a vector. First, the cross product isn’t associative: order matters. next, remember what the cross product is doing: finding orthogonal vectors. if any two components are parallel ($\vec{a}$ parallel to $\vec{b}$) then there are no dimensions pushing on each other, and the cross product is zero (which carries through to $0 \times \vec{c}$). Given two non parallel, nonzero vectors \(\vec u\) and \(\vec v\) in space, it is very useful to find a vector \(\vec w\) that is perpendicular to both \(\vec u\) and \(\vec v\). there is a operation, called the cross product, that creates such a vector. this section defines the cross product, then explores its properties and applications. To include an example for calculating the cross product of two vectors, we will use the vectors a = (2, 3, 7) and b = (1, 2, 4). the first step is to introduce the components of vector a. that is: x = 2, y = 3 and z = 7. next, you should introduce the components of vector b. that is: x = 1, y = 2 and z = 4.

Cross Product Two Dimensions Given two non parallel, nonzero vectors \(\vec u\) and \(\vec v\) in space, it is very useful to find a vector \(\vec w\) that is perpendicular to both \(\vec u\) and \(\vec v\). there is a operation, called the cross product, that creates such a vector. this section defines the cross product, then explores its properties and applications. To include an example for calculating the cross product of two vectors, we will use the vectors a = (2, 3, 7) and b = (1, 2, 4). the first step is to introduce the components of vector a. that is: x = 2, y = 3 and z = 7. next, you should introduce the components of vector b. that is: x = 1, y = 2 and z = 4.