Matrices Matrix Transformations

Transformation Matrices Summary By Jennyf100 Teaching Resources Tes The mathematics. for each [x,y] point that makes up the shape we do this matrix multiplication: when the transformation matrix [a,b,c,d] is the identity matrix (the matrix equivalent of "1") the [x,y] values are not changed: changing the "b" value leads to a "shear" transformation (try it above): and this one will do a diagonal "flip" about the. Figure 3.1.20 : a picture of the matrix transformation t. the input vector is x, which is a vector in r3, and the output vector is b = t(x) = ax, which is a vector in r2. the violet line on the right is the range of t; as you vary x, the output b is constrained to lie on this line.
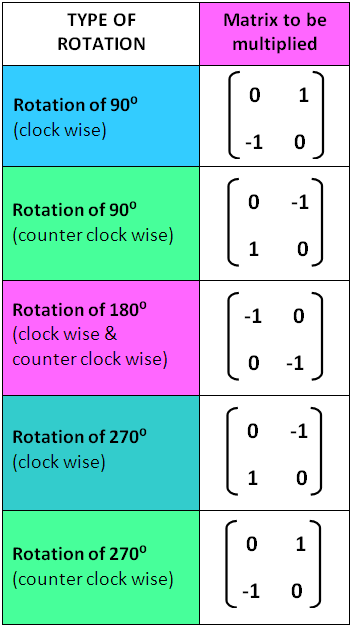
Rotation Transformation Matrix Matrices can be used to perform a wide variety of transformations on data, which makes them powerful tools in many real world applications. for example, matrices are often used in computer graphics to rotate, scale, and translate images and vectors. they can also be used to solve equations that have multiple unknown variables (x, y, z, and more) and they do it very efficiently!. The linearity of matrix vector multiplication proposition 2.2.3 provides the key to answering this question. remember that if a is a matrix, v and w vectors, and c a scalar, then. a(cv) = cav a(v w) = av aw this means that a matrix transformation t(x) = ax satisfies the corresponding linearity property:. Multiplication as a transformation. the idea of a "transformation" can seem more complicated than it really is at first, so before diving into how 2 × 2 matrices transform 2 dimensional space, or how 3 × 3 matrices transform 3 dimensional space, let's go over how plain old numbers (a.k.a. 1 × 1 matrices) can be considered transformations. The matrix transformation associated to a is the transformation. t : r n −→ r m debnedby t ( x )= ax . this is the transformation that takes a vector x in r n to the vector ax in r m . if a has n columns, then it only makes sense to multiply a by vectors with n entries. this is why the domain of t ( x )= ax is r n .

Transformation Matrix Definition Formula Applications Examples Multiplication as a transformation. the idea of a "transformation" can seem more complicated than it really is at first, so before diving into how 2 × 2 matrices transform 2 dimensional space, or how 3 × 3 matrices transform 3 dimensional space, let's go over how plain old numbers (a.k.a. 1 × 1 matrices) can be considered transformations. The matrix transformation associated to a is the transformation. t : r n −→ r m debnedby t ( x )= ax . this is the transformation that takes a vector x in r n to the vector ax in r m . if a has n columns, then it only makes sense to multiply a by vectors with n entries. this is why the domain of t ( x )= ax is r n . Matrix transformations. in the preview activity, we considered simple linear functions, such as g(x) = 1 2x whose graph is the line shown in figure 2.5.3. we construct a function like this by choosing a number m; when given an input x, the output g(x) = mx is formed by multiplying x by m. figure 2.5.3. For any linear transformation t we can find a matrix a so that t(v) = av. if the transformation is invertible, the inverse transformation has the matrix a−1. the product of two transformations t1: v → a1v and t2: w → a2w corresponds to the product a2 a1 of their matrices. this is where matrix multi plication came from! 4.
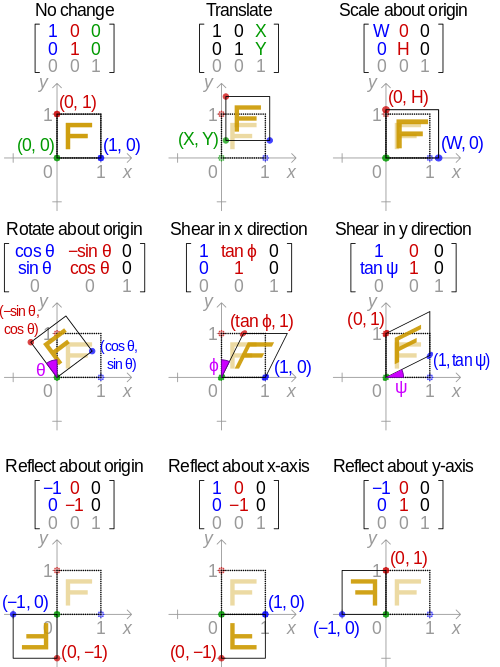
Matrice De Transformation Transformation Matrix Abcdef Wiki Matrix transformations. in the preview activity, we considered simple linear functions, such as g(x) = 1 2x whose graph is the line shown in figure 2.5.3. we construct a function like this by choosing a number m; when given an input x, the output g(x) = mx is formed by multiplying x by m. figure 2.5.3. For any linear transformation t we can find a matrix a so that t(v) = av. if the transformation is invertible, the inverse transformation has the matrix a−1. the product of two transformations t1: v → a1v and t2: w → a2w corresponds to the product a2 a1 of their matrices. this is where matrix multi plication came from! 4.

Reflection Transformation Matrix

Comments are closed.