Solved Prove That The Polar Form Of The Cauchy Riemann Chegg

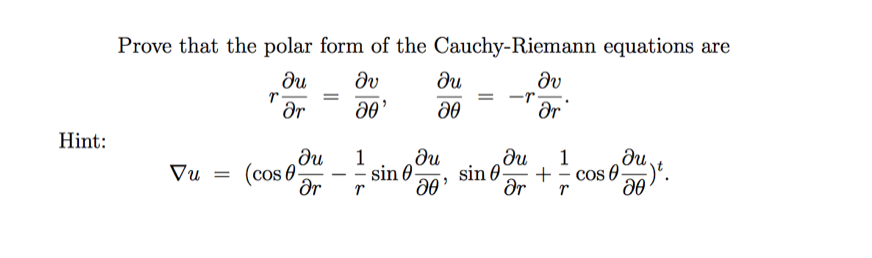
Solved Prove That The Polar Form Of The Cauchy Riemann Chegg Math; advanced math; advanced math questions and answers; prove that the polar form of the cauchy riemann equations are r partial differential u partial differential r = partial differential v partial differential theta, partial differential u partial differential theta = r partial differential v partial differential r. Prove that in polar form the cauchy riemann equations can be written = @o this problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts.

Solved The Cauchy Riemann Equations In Polar Form Are Given Cheggођ The polar form of the cauchy riemann equations. (a) use the coordinate transformation x=rcosθ and y=rsinθ and the chain rules ur=ur∂r∂x uy∂r∂y and uθ=ux∂θ∂x uy∂θ∂y etc. to prove that ur=u3cosθ uysinθ and u0=−uxrsinθ uyrcosθvr=vxcosθ vysinθ and vθ=−vrrsinθ vyrcosθ (b) use the results of part (a) to prove that. Show that in polar coordinates, the cauchy riemann equations take the form ∂u ∂r = 1 r ∂v ∂θ and 1 r∂u ∂θ = − ∂v ∂r. use these equations to show that the logarithm function defined by logz = logr iθ where z = reiθ with − π <θ <π is holomorphic in the region r> 0 and − π <θ <π. what i have so far:. The cauchy riemann equations provide us with a direct way of checking that a function is differen tiable and computing its derivative. example \ (\pageindex {1}\) use the cauchy riemann equations to show that \ (e^z\) is differentiable and its derivative is \ (e^z\). Cauchy riemann equations in polar form (10.7) at (r 0; 0). moreover, if a mapping f(rej ) = u(r; ) jv(r; ) is di erentiable at a point z 0 = r 0ej 0, its derivative at that point is given by either expression in (10.6). example 10.2. the principal logarithm is a good example of a function that is best expressed in polar form.

Solved Show That In Polar Coordinates Cauchy Riemann Chegg The cauchy riemann equations provide us with a direct way of checking that a function is differen tiable and computing its derivative. example \ (\pageindex {1}\) use the cauchy riemann equations to show that \ (e^z\) is differentiable and its derivative is \ (e^z\). Cauchy riemann equations in polar form (10.7) at (r 0; 0). moreover, if a mapping f(rej ) = u(r; ) jv(r; ) is di erentiable at a point z 0 = r 0ej 0, its derivative at that point is given by either expression in (10.6). example 10.2. the principal logarithm is a good example of a function that is best expressed in polar form. Theorem. let d ⊆ c be an open subset of the set of complex numbers c. let f: d → c be a complex function on d. let u, v: {(x, y) ∈ r2: x iy = z ∈ d} → r be the two real valued functions defined as: where: the cauchy riemann equations can be expressed in polar form as: where z is expressed in exponential form as:. Often, the easiest way to prove that a function is analytic in a given domain is to prove that the cauchy riemann equations are satisfied. example 7.3.1. we can use the cauchy riemann equations to prove that the function f(z) = 1 z is analytic everywhere, except at z = 0. let us write the function as f(x iy) = 1 x iy = x − iy x2 y2.

Solved Polar Form Of The Cauchy Riemann Equations Let Zo E Chegg Theorem. let d ⊆ c be an open subset of the set of complex numbers c. let f: d → c be a complex function on d. let u, v: {(x, y) ∈ r2: x iy = z ∈ d} → r be the two real valued functions defined as: where: the cauchy riemann equations can be expressed in polar form as: where z is expressed in exponential form as:. Often, the easiest way to prove that a function is analytic in a given domain is to prove that the cauchy riemann equations are satisfied. example 7.3.1. we can use the cauchy riemann equations to prove that the function f(z) = 1 z is analytic everywhere, except at z = 0. let us write the function as f(x iy) = 1 x iy = x − iy x2 y2.