Solved Use Limits To Determine Any Horizontal Asymptotes For The Graph

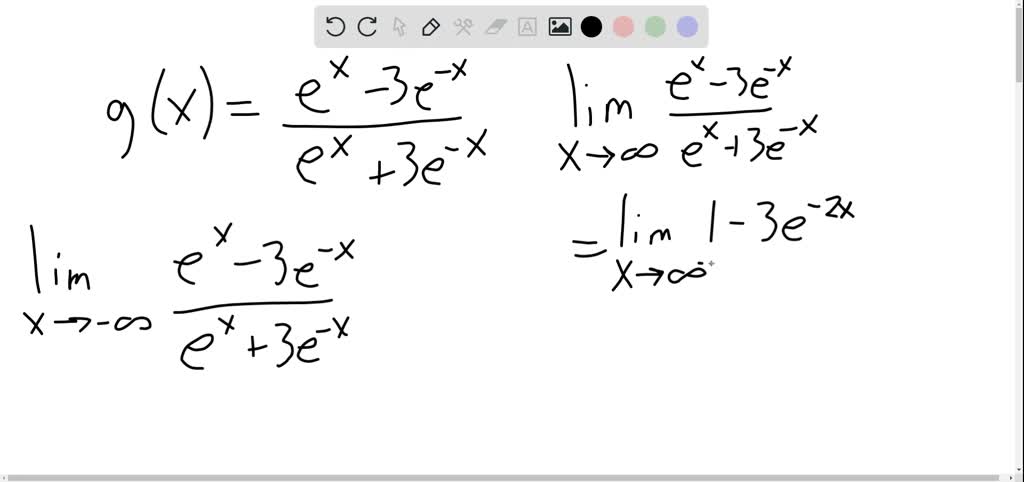
Solved Use Limits To Determine Any Horizontal Asymptotes For The Graph Find all horizontal asymptote(s) of the function $\displaystyle f(x) = \frac{x^2 x}{x^2 6x 5}$ and justify the answer by computing all necessary limits. also, find all vertical asymptotes and justify your answer by computing both (left right) limits for each asymptote. my answer so far. Step 1: find lim ₓ→∞ f (x). i.e., apply the limit for the function as x→∞. step 2: find lim ₓ→ ∞ f (x). i.e., apply the limit for the function as x→ ∞. step 3: if either (or both) of the above limits are real numbers then represent the horizontal asymptote as y = k where k represents the value of the limit.

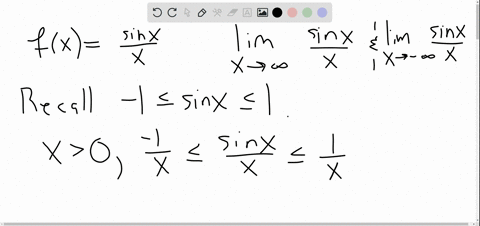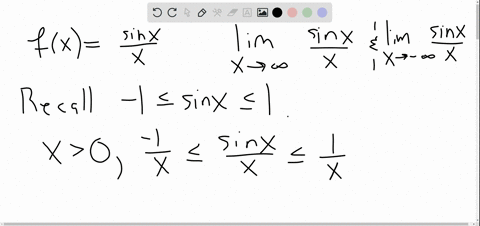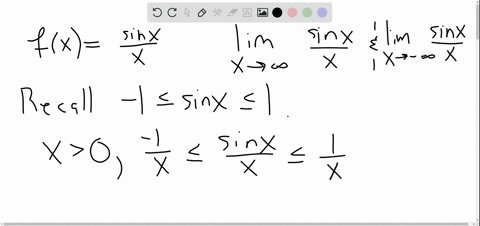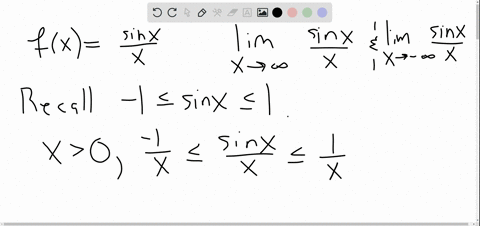
Solved Use Limits To Determine Any Horizontal Asymptotes For The Graph Graphically, it concerns the behavior of the function to the "far right'' of the graph. we make this notion more explicit in the following definition. definition 6: limits at infinity and horizontal asymptote. we say lim x → ∞f(x) = l if for every ϵ> 0 there exists m> 0 such that if x ≥ m, then | f(x) − l | <ϵ. From its graph we see that as the values of x approach 2, the values of h(x) = 1 (x − 2)2 become larger and larger and, in fact, become infinite. mathematically, we say that the limit of h(x) as x approaches 2 is positive infinity. symbolically, we express this idea as. lim x → 2h(x) = ∞. more generally, we define infinite limits as. Horizontal asymptote. horizontal asymptotes, or ha, are horizontal dashed lines on a graph that help determine the end behavior of a function. they show how the input influences the graph’s curve as it extends toward infinity. mathematically, they can be represented as the equation of a line y = b when either lim x → ∞ = b or lim x →. We can extend this idea to limits at infinity. for example, consider the function f(x) = 2 1 x. as can be seen graphically in figure 1.4.1 and numerically in table 1.4.1, as the values of x get larger, the values of f(x) approach 2. we say the limit as x approaches ∞ of f(x) is 2 and write lim x → ∞ f(x) = 2.