Solved Vector Cross Product 6 Of 11 Let Vectors Chegg

Solved Vector Cross Product 6 Of 11 Let Vectors Chegg Vector cross product 6 of 11 let vectors a = (1, 0, − 3), b = (− 2, 5, 1), and c = (3, 1, 1). calculate the following, expressing your answers as ordered triples (three commaseparated numbers). v 1 and v 2 are perpendicular, part g if v 1 and v 2 are parallel,. Our expert help has broken down your problem into an easy to learn solution you can count on. question: vector cross product let vectors a⃗ = (1,0,−3), b⃗ = (−2,5,1), and c⃗ = (3,1,1). calculate the following, expressing your answers as ordered triples (three comma separated numbers). part a b⃗ ×c⃗ = part b c⃗ ×b⃗ = part c.

Solved 6 Consider The Vectors Vi 11 11 For What Value S Chegg 49) consider \(\vecs u\) and \(\vecs v\) two three dimensional vectors. if the magnitude of the cross product vector \(\vecs u×\vecs v\) is \( k\) times larger than the magnitude of vector \(\vecs u\), show that the magnitude of \(\vecs v\) is greater than or equal to \( k\), where \( k\) is a natural number. Free vector cross product calculator find vector cross product step by step vectors are used to represent anything that has a direction and magnitude, length. The first step is to redraw the vectors →a and →b so that the tails are touching. then draw an arc starting from the vector →a and finishing on the vector →b . curl your right fingers the same way as the arc. your right thumb points in the direction of the vector product →a × →b (figure 3.28). figure 3.28: right hand rule. Using equation 2.9 to find the cross product of two vectors is straightforward, and it presents the cross product in the useful component form. the formula, however, is complicated and difficult to remember. fortunately, we have an alternative. we can calculate the cross product of two vectors using determinant notation.

Solved Vector Cross Product For The Vectors Shown In The Chegg The first step is to redraw the vectors →a and →b so that the tails are touching. then draw an arc starting from the vector →a and finishing on the vector →b . curl your right fingers the same way as the arc. your right thumb points in the direction of the vector product →a × →b (figure 3.28). figure 3.28: right hand rule. Using equation 2.9 to find the cross product of two vectors is straightforward, and it presents the cross product in the useful component form. the formula, however, is complicated and difficult to remember. fortunately, we have an alternative. we can calculate the cross product of two vectors using determinant notation. [contrast section 11.3 theorem 11.6, a b a b cos θ r r r r • = .] the text does the proof using the definitions of dot product and cross product. extending theorem 11.10b to the case in which θ = 0 or θ = π, we get corollary 11.11. corollary 11.11: two nonzero vectors are parallel iff 0 r r a×b = . [note this is the vector 0 r.] example. When the angle between \(\vec u\) and \(\vec v\) is 0 or \(\pi\) (i.e., the vectors are parallel), the magnitude of the cross product is 0. the only vector with a magnitude of 0 is \(\vec 0\) (see property 9 of theorem 84), hence the cross product of parallel vectors is \(\vec 0\). we demonstrate the truth of this theorem in the following example.

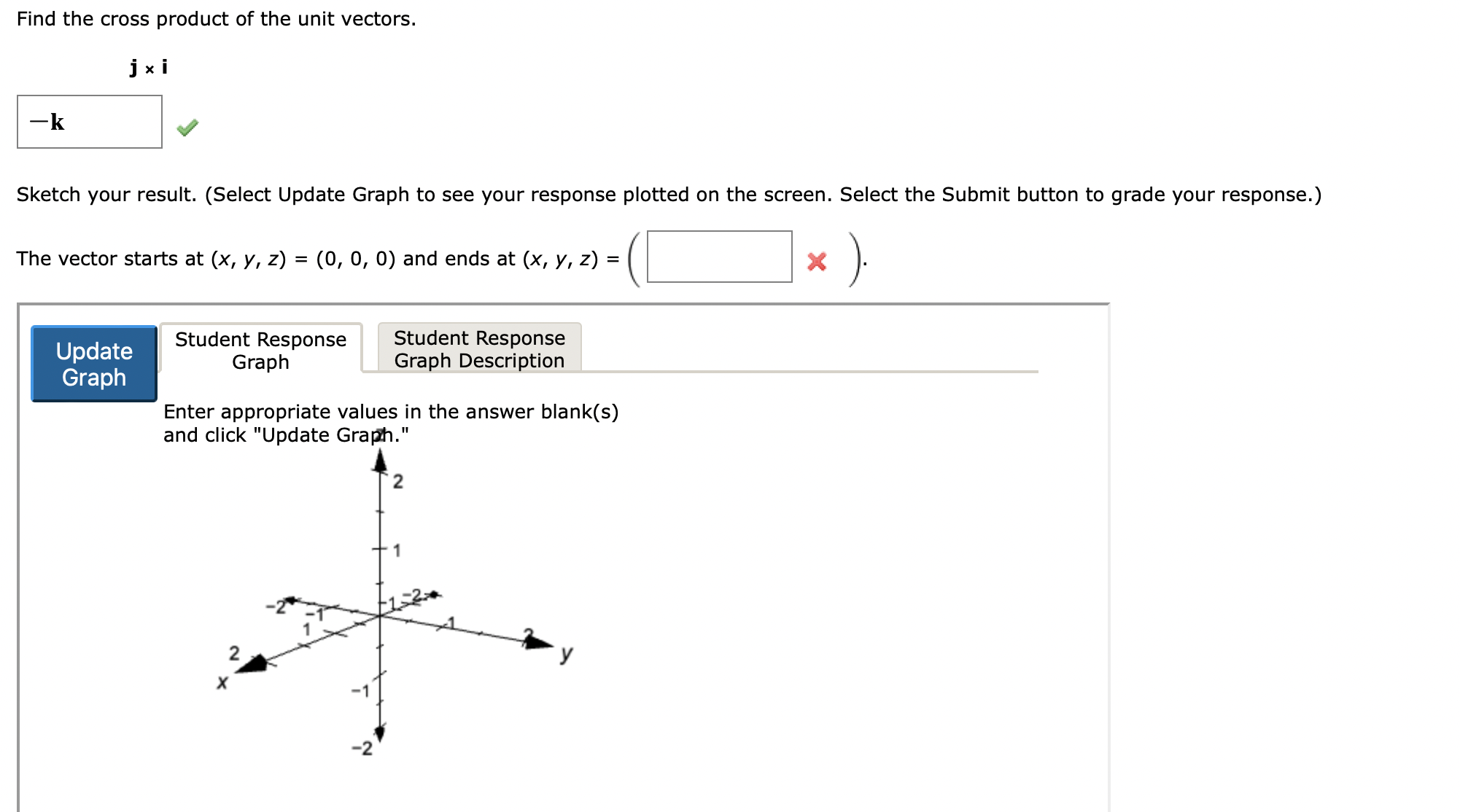
Solved Find The Cross Product Of The Unit Vectors Jг I Chegg [contrast section 11.3 theorem 11.6, a b a b cos θ r r r r • = .] the text does the proof using the definitions of dot product and cross product. extending theorem 11.10b to the case in which θ = 0 or θ = π, we get corollary 11.11. corollary 11.11: two nonzero vectors are parallel iff 0 r r a×b = . [note this is the vector 0 r.] example. When the angle between \(\vec u\) and \(\vec v\) is 0 or \(\pi\) (i.e., the vectors are parallel), the magnitude of the cross product is 0. the only vector with a magnitude of 0 is \(\vec 0\) (see property 9 of theorem 84), hence the cross product of parallel vectors is \(\vec 0\). we demonstrate the truth of this theorem in the following example.