Use Substitution To Evaluate Integral Sin 3 2x Dx Use Trig

Use Substitution To Evaluate Integral Sin 3 2x Dx Use Trig Identity Trigonometric\:substitution\:\int 50x^ {3}\sqrt {1 25x^ {2}}dx. integrate functions using the trigonometric substitution method step by step. advanced math solutions – integral calculator, advanced trigonometric functions. in the previous post we covered substitution, but substitution is not always straightforward, for instance integrals. Integrate using trigo substitution int dx (sqrt (x^2 4x))^3 ? by changing variables, integration can be simplified by using the substitutions x=a\sin (\theta), x=a\tan (\theta), or x=a\sec (\theta). once the substitution is made the function can be simplified using basic trigonometric identities.

Trigonometric Substitution Definition Integration Examples Section 7.3 : trig substitutions. as we have done in the last couple of sections, let’s start off with a couple of integrals that we should already be able to do with a standard substitution. ∫x√25x2 − 4dx = 1 75(25x2 − 4)3 2 c ∫ x √25x2 − 4 dx = 1 25√25x2 − 4 c. both of these used the substitution u = 25x2 − 4 and at. This video works out the integral of sin^3(2x). this is a u substitution trig integral which would typically be found in a calculus 1 class.#calculus #trigi. Figure 7.3.7: calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. we can see that the area is a = ∫5 3√x2 − 9dx. to evaluate this definite integral, substitute x = 3secθ and dx = 3secθtanθdθ. we must also change the limits of integration. Integrating expressions involving a 2 x 2 a 2 x 2. for integrals containing a 2 x 2, a 2 x 2, let’s first consider the domain of this expression. since a 2 x 2 a 2 x 2 is defined for all real values of x, x, we restrict our choice to those trigonometric functions that have a.

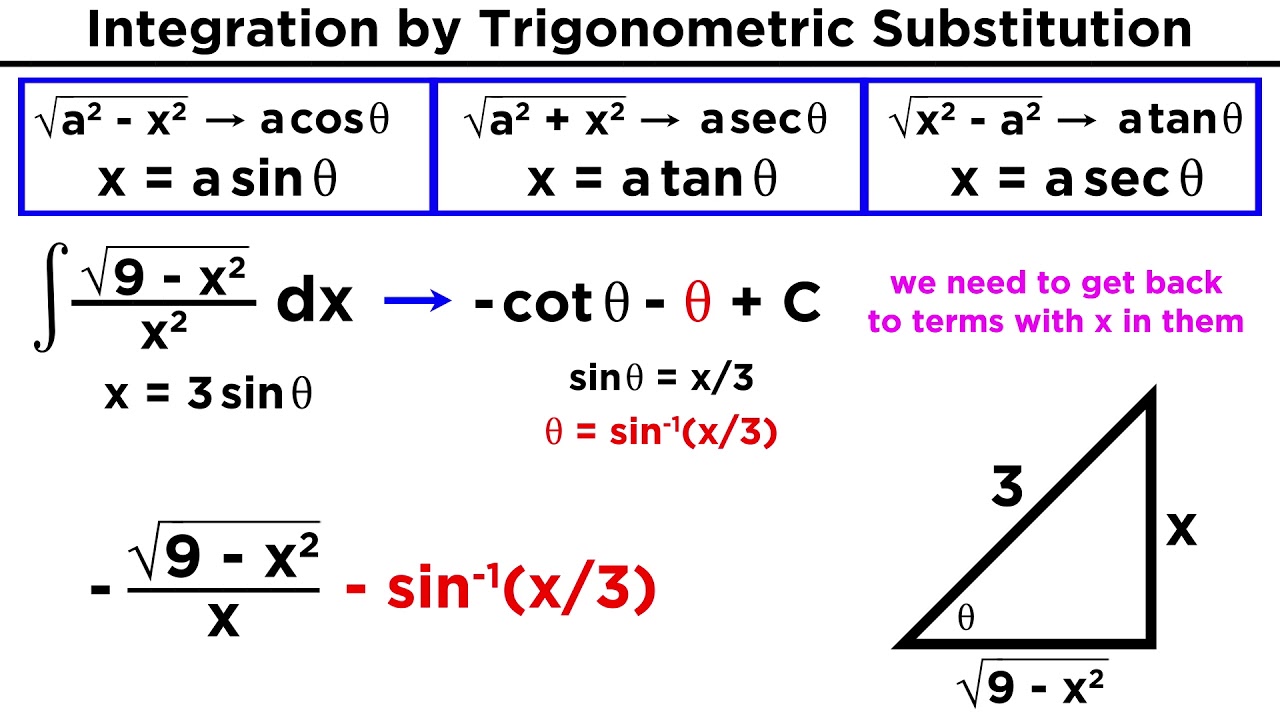
Integration By Trigonometric Substitution Youtube Figure 7.3.7: calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. we can see that the area is a = ∫5 3√x2 − 9dx. to evaluate this definite integral, substitute x = 3secθ and dx = 3secθtanθdθ. we must also change the limits of integration. Integrating expressions involving a 2 x 2 a 2 x 2. for integrals containing a 2 x 2, a 2 x 2, let’s first consider the domain of this expression. since a 2 x 2 a 2 x 2 is defined for all real values of x, x, we restrict our choice to those trigonometric functions that have a. Mc ty intusingtrig 2009 1. some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. these allow the integrand to be written in an alternative form which may be more amenable to integration. on occasions a trigonometric substitution will enable an integral to be evaluated. Example 6.4.4: using trigonometric substitution. evaluate ∫ √4 − x2 x2 dx. solution. we use key idea 13 (a) with a = 2, x = 2sinθ, dx = 2cosθ and hence √4 − x2 = 2cosθ. this gives. ∫√4 − x2 x2 dx = ∫ 2cosθ 4sin2θ(2cosθ) dθ = ∫cot2θ dθ = ∫(csc2θ − 1) dθ = − cotθ − θ c. we need to rewrite our answer in.

Integral Of Sin 3 2x Using Multiple Substitutions Youtube Mc ty intusingtrig 2009 1. some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. these allow the integrand to be written in an alternative form which may be more amenable to integration. on occasions a trigonometric substitution will enable an integral to be evaluated. Example 6.4.4: using trigonometric substitution. evaluate ∫ √4 − x2 x2 dx. solution. we use key idea 13 (a) with a = 2, x = 2sinθ, dx = 2cosθ and hence √4 − x2 = 2cosθ. this gives. ∫√4 − x2 x2 dx = ∫ 2cosθ 4sin2θ(2cosθ) dθ = ∫cot2θ dθ = ∫(csc2θ − 1) dθ = − cotθ − θ c. we need to rewrite our answer in.